Les Modèles Génératifs (Partie 2) | Generative Adversial Network (GAN)

Sommaire

1. Introduction

Les GANs sont une approche de la modélisation générative utilisant des méthodes d’apprentissage en profondeur tels que les réseaux de neurones convolutifs. Les GANs forment un modèle génératif composé de deux sous-modèles:

• Modèle générateur qui génère de nouveaux exemples qui ressemblent aux exemples du dataset d’apprentissage.
• Modèle discriminateur qui tente de classer les exemples comme réels (dataset d’apprentissage) ou faux (généré).

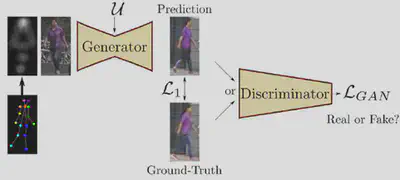
Ces deux sous-modèles sont entraînés ensemble dans un jeu à somme nulle. Le discriminateur cherche à maximiser ses actions de classification tandis que le générateur tente de minimiser ses actions pour tromper le discriminateur. Ainsi le discriminateur est mis à jour avec la méthode du gradient ascendant (on cherche le maximum global) alors que le générateur est mis à jour avec la méthode du gradient descendant (on cherche le minimum global). L’apprentissage du modèle GAN converge lorsque le discriminateur et le générateur atteignent l’équilibre de Nash qui correspond au point optimal pour le jeu à somme nulle (le générateur ne changera pas son action indépendamment de la décision prise par le discriminateur).

2. Fonction Objective : Minimax

Les GANs sont difficiles à entraîner dû à des problèmes de non-convergences:

Fonction objective : Minimax

$$ $\min _{\theta_{g}} \max _{\theta_{d}}\left[\mathbb{E}_{x \sim p_{\text {data }}} \log D_{\theta_{d}}(x)+\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)\right] $$

1. Gradient descendant pour le générateur $$ \min_{\theta_{g}} \mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right) $$

2. Gradient ascendant pour le discriminateur

$$ \max_{\theta_{d}}\left[\mathbb{E}_{x \sim p_{\text {data }}} \log D_{\theta_{d}}(x)+\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)\right] $$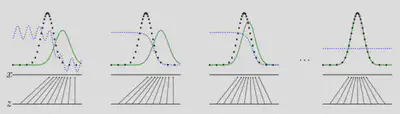

Le rôle du discriminateur est de maximiser la fonction suivante $D(x) - D(G(z))$ qui consiste à maximiser la différence entre sa sortie pour les vraies données et celle pour les données générées. Le rôle du générateur est de maximiser la fonction $D(G(z))$ afin de maximiser la sortie du discriminateur pour les données qu’il génère, et ainsi minimiser leur distance avec les vraies données.

3. Les limites d’un GAN

Le GAN fait face à deux limites majeures qui sont les suivantes:

Le mode collapse

Le générateur génère une diversité d’échantillon limitée (i.e Le générateur finit par ne modéliser qu’un petit sous-ensemble des données d’apprentissage de formation) ce qui amène le générateur à être paresseux dans son entraînement.

La disparition du gradient

La disparition du gradient est souvent recontrée dans le cadre des GANs lorsque la fonction de perte du générateur se rapproche de $0$ ce qui le rend diffcile en entraîner. Ce phénomène peut apparaître si :

• Le discriminateur se trompe alors le générateur reçoit un mauvais retour
• Le discriminateur ne se trompe jamais, le générateur n’apprend plus

4. Les métriques pour contrer les limites

Certaines métriques permettent de contrer les problèmes mentionnées précéemment selon certains compromis :

• Kullback-Leibler élimine la disparition du gradient mais favorise un effondrement de mode (le générateur est restreint à générer qu’un seul type d’exemple)
  

• Wasserstein améliore la stabilité de l’entraînement mais favorise la non-convergence vers l’équilibre de Nash. En effet, la perte de Wasserstein permet au discriminateur d’apprendre à rejeter les éléments générés sur lesquels le générateur se stabilise. Et ainsi, permettre au générateur d’essayer des nouvelles propositions (générer de nouveaux exemples) pour se diversifier.

Correspondance des caractéristiques

Problème :

• Le générateur essaie de trouver la meilleure image pour tromper le discriminateur.
• La “meilleure” image change constamment lorsque les deux réseaux contrecarrent leur adversaire.
• Le modèle ne converge pas et le mode s’effondre.

Ajouter une perte pour la correspondance des caractéristiques élargit l’objectif de battre l’adversaire à la correspondance des caractéristiques dans des images réelles.

Discrimination par mini-lots

• Calculer la similarité $o(x)$ de l’image x avec les images du même lot. Ajoutez la similarité $o(x)$ dans l’une des couches denses dans le discriminateur pour classer si cette image est réelle ou générée.
  

• Si le mode commence à s’effondrer, la similarité des images générées augmente. Le discriminateur peut utiliser $o(x)$ pour détecter les images générées et pénaliser le générateur si le mode s’effondre.

Améliorer l’entraînement des GANs

• Utiliser la Batch normalization pour stabiliser l’entraînement et ainsi obtenir une meilleure généralisation
• Modifier la fonction de perte du réseau (par exemple en utilisant la perte de Wasserstein).

5. Processus de fonctionnement d’un GAN

Le processus de fonctionnement d’un GAN est le suivant :

1. On constitue un jeu d’entraînement qui comporte une multitude d’images qui sont annotés avec le label True
   

2. On constitue un jeu d’entraînement composés de plusieurs images fictives construites par le générateur auxquelles on associe le label False
   

3. On fusionne les deux jeux d’entraînement pour entraîner le discriminateur à prédire correctement les labels des images. Pour cela le discriminateur apprend en fait une probabilité pour une image d’être vraie
   

4. On arrête l’entraînement du discriminateur et on l’immobilise dans cet état.
   

5. On entraîne le générateur à tromper le discriminateur : Le générateur fabrique de nouvelles images fictives et soumet ces dernières au discriminateur
   

6. On optimise le générateur jusqu’à ce que le discriminateur attribue à tort le label True aux images fictives le plus souvent possibles.
   

En réitérant ce processus, le générateur va produire des images fictives de plus en plus réalistes ce qui permettra ainsi à améliorer le discernement du discriminateur et contraindra le générateur à s’améliorer également pour tromper le discriminateur en produisant des images indiscernables pour ce dernier.

6. Evaluer les performances d’un GAN

L’inception Score permet d’évaluer les performances d’un GAN. L’idée clé est que le générateur doit produire des images avec une variété de classes d’objets reconnaissables selon deux critères:

• Un humain, regardant une image distincte, serait en mesure de déterminer avec confiance ce qui s’y trouve (saillance).
  

• Un humain, regardant un ensemble d’images diverses, dirait que l’ensemble comporte beaucoup d’objets différents (diversité)

Inception Score

$$ IS(G)=\exp \left(\mathbb{E}_{\mathbf{x} \sim p_{a}} D_{K L}(p(y \mid \mathbf{x}) \| p(y))\right) $$

où $p(y|x)$ est la distribution postérieure de l’étiquette renvoyée par un classifieur d’images (par ex, InceptionNet) pour l’échantillon $x$. La divergence KL est une mesure de similarité entre deux distributions de probabilité.

• Si l’image contient un objet reconnaissable, l’entropie de $p(y|x)$ devrait être faible.
• Si le générateur génère des images d’objets divers, la distribution marginale $p(y)$ devrait avoir une entropie élevée.
• Inconvénient : un GAN qui se contente de mémoriser les données d’apprentissage (surajustement) ou qui produit en sortie une seule image par classe (abandon de mode) pourrait tout de même obtenir de bons résultats.

En résumé, la divergence KL est élevée lorsque nos distributions sont dissemblables. C’est-à-dire qu’elle est élevée lorsque chaque image générée a une étiquette distincte et que l’ensemble des images générées a un éventail diversifié d’étiquettes.

Pour obtenir le score final, nous prenons l’exponentielle de la divergence KL afin de faire croître le score vers de plus grands nombres pour qu’il soit plus facile de le voir s’améliorer. Enfin nous prenons la moyenne de ceci pour toutes nos images. Le résultat est le score d’Inception !