Les Modèles Génératifs (Partie 1) | Auto-Encodeur (AE) & Variational Auto-Encodeur (VAE)

Sommaire

1. Généralités

L’auto-encodeur est un modèle génératif qui a pour but d’apprendre une distribution approchée d’un ensemble de points ayant une distribution inconnue.

L’auto encodeur comporte :

• Un encodeur qui compresse et stocke l’in contenu dans les données au sein de plusieurs variables latentes.
• Un décodeur qui va reconstruire (décompresser) l’in compressé par l’encodeur de la manière la plus fidèle possible

L’encodeur apprend à conserver autant d’ins pertinentes que possible dans l’encodage limité et à éliminer intelligemment les parties non pertinentes. Le décodeur apprend à prendre l’encodage et à le reconstruire correctement en une image complète.

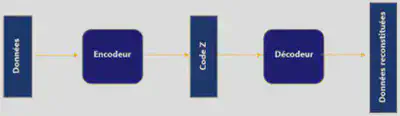
Les auto-encodeurs utilisent une architecture de réseaux de neurones particulière pour réaliser une réduction de dimension. Effectuer une réduction de dimension revient à projeter une base d’exemples de grande dimension dans un espace de plus petite dimension. Cette technique permet de compresser des données.

2. Architecture d’un Auto-Encodeur (AE)

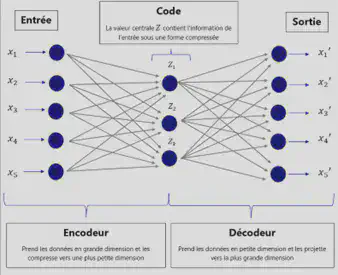
L’architecture d’un auto-encodeur prend la forme d’un diabolo car elle possède un centre resserré avec des entrées et des sorties élargies. Grâce à cette architecture, l’encodeur est capable de représenter par exemple une image tout entière grâce à un minimum de points sur un plan 2D. Cette architecture constitue une étape préliminaire de traitement de données ce que l’on appelle l’extraction de caractéristiques. Généralement, le réseau de neurones attaque directement les données brutes pour réaliser par lui-même l’extraction de caractéristique. En fait, de manière plus concrète, les auto-encodeurs sont des modèles d’apprentissage non supervisé qui utilisent des variables latentes pour décrire et contenir l’in de chaque pixel d’une image.

3. L’espace latent

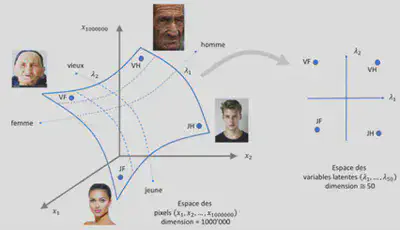
Pour expliquer cette notion de variables latentes, prenons l’exemple d’une collection d’images de visages humains d’une résolution 1000x1000 pixels. Nous avons donc un espace de dimension 1 000 000. Les paramètres tels que l’âge, le sexe, la coupe de cheveux, le teint, le sourire,… ne sont pas suffisant pour décrire correctement un visage en particulier. L’algorithme va donc prendre en entrée les 1 000 000 pixels qui sont stockés dans les variables $x_{1},x_{2},x_{3},…,x_{1000000}$. Toutes ces variables sont en fait les paramètres qui sont fournis à l’entrée de l’algorithme du réseau de neurones. Cependant tous ces paramètres ne sont pas tous nécessaires pour l’algorithme. En effet, seulement un certain nombre de pixels peut servir à décrire les visage humains de notre exemple. Ainsi une réduction de dimension peut être envisagée. On peut par exemple émettre l’hypothèse que seulement 50 variables correspondent à des visages humains. Ce sont ces 50 variables que l’on appelle: les variables latente $\lambda_{1},λ_{2},λ_{3},…λ_{50}$. Ces dernières correspondent finalement à une forme compressée de l’in visuelle. Cela aboutit à la création d’un espace de plus faible dimension constitué de différents points et chaque point de cet espace correspond à un visage. Les coordonnées sont les variables latentes.

4. L’apprentissage d’un Auto-Encodeur

Si nous résumons, nous venons de voir qu’un auto-encodeur est capable de reconstruire un espace de variables latentes. Cependant les différentes variables latentes que l’algorithme découvre ne peuvent pas être interprétables directement. Par exemple, reconstruire une image à partir d’un point dans l’espace latent.

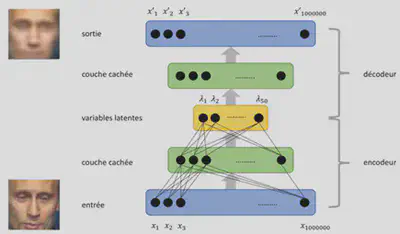
Plus le nombre de couches et de neurones sont importants, plus l’auto-encodeur sera en mesure d’encoder et décoder des images complexes. Le nombre de neurones de la couche centrale correspond au nombre de variables latentes que l’on souhaite découvrir. Le nombre de variables latentes sont ce que l’on appelle des hyperparamètres. Il est nécessaire d’ajuster ces hyperparamètres par tâtonnement pour obtenir une reconstruction optimale sans trop de ressource.

L’ensemble du réseau est généralement formé dans son ensemble. La fonction de perte est généralement soit l’erreur quadratique moyenne, soit l’entropie croisée entre la sortie et l’entrée, connue sous le nom de perte de reconstruction, qui pénalise le réseau pour la création de sorties différentes de l’entrée.

Pour apprendre, un auto-encodeur se base sur un modèle d’apprentissage non supervisé. Pour entraîner un auto-encodeur, on doit fournir à ce dernier une série d’exemples en entrée en lui demandant d’apprendre à reproduire ces exemples de manière la plus fidèle sur la couche de sortie tout en minimisant une erreur de reconstruction. Cette erreur est calculée par la fonction de coût d’erreur de reconstruction qui évalue la différence entre l’image originale et l’image reconstruite. L’encodeur se charge alors de compresser l’information et de la stocker avec le moins de variables latentes possibles. Le décodeur lui se chargera de reconstruire l’image du mieux qu’il peut. On peut remarquer tout de même un goulot d’étranglement au niveau de la couche dédiée aux variables latentes. En effet, le nombre de variables latentes contraint l’auto-encodeur à trouver une représentation parcimonieuse des données qui l’on été fournies en entrée.

Il s’avère que le mécanisme de compression de l’information fonctionne correctement uniquement sur les données de même nature que celles avec lesquelles on a entraîné l’auto-encodeur.

Une façon de forcer l’auto-codeur à apprendre des caractéristiques utiles consiste à ajouter un bruit aléatoire à ses entrées et en lui faisant récupérer les données originales sans bruit.

5. Une amélioration de l’Auto-Encodeur : L’Auto-Encodeur Variationnel

Il s’avère en pratique que les auto-encodeurs tels qu’ils ont été présentés précédemment fonctionnent mal. L’auto-encodeur variationnel est une amélioration de l’auto-encodeur et intégre 2 ajouts.

1er ajout :

Au lieu d’encoder chaque image par un point $\lambda$ dans l’espace latent comme le fait l’auto-encodeur simple, un auto-encodeur variationnel choisi au hasard un point $\lambda^{’}$ proche du point $\lambda$. Pour ce faire, l’auto-encodeur variationnel calcule une distribution de probabilité centrée sur $\lambda$ et d’écart type $\sigma$, les deux étant appris par l’encodeur. Ainsi l’auto-encodeur variationnel comporte 2 modules distincts : un module qui calcule la moyenne et un autre module qui calcul variance d’une distribution normale. Ce processus conduit à flouter l’image et contraint l’auto-encodeur variationnel à découvrir des encodages plus efficaces pouvant aboutir à une représentation plus fidèle que la représentation parcimonieuse apprise par un auto-encodeur standard.

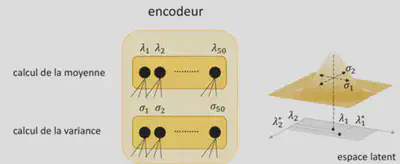
2ème ajout :

L’ensemble des points associés à toutes les images de l’ensemble d’entraînement forment un nuage de points dans l’espace latent. On peut penser que la forme de ce nuage est arbitraire. Or pour forcer le nuage de point à avoir une forme simple (loi normale) l’auto-encodeur intègre en plus de la fonction de coût d’erreur de reconstruction, une fonction de coût qui corrige la forme du nuage si la distribution des points s’éloigne trop d’une loi normale standard.

Puisque nous modélisons la génération probabiliste des données, les réseaux de codeurs et de décodeurs sont probabilistes.

Intuitivement, le vecteur moyenne $\mu$ contrôle l’endroit où l’encodage d’une entrée doit être centré, tandis que l’écart type $\sigma$ contrôle la “zone”, dans quelle mesure l’encodage peut varier par rapport à la moyenne. Comme les encodages sont générés au hasard à partir de n’importe où à l’intérieur du “cercle” (la distribution), le décodeur apprend que non seulement un point unique dans l’espace latent se réfère à un échantillon de cette classe, mais que tous les points proches se réfèrent également à la même chose. Cela permet au décodeur non seulement de décoder des codages uniques et spécifiques dans l’espace latent (laissant l’espace latent décodable discontinu), mais aussi ceux qui varient légèrement, car le décodeur est exposé à une gamme de variations du codage de la même entrée pendant entraînement.

Ce que nous voulons idéalement, ce sont des encodages, qui soient tous aussi proches que possible les uns des autres tout en étant distincts, permettant une interpolation fluide et permettant la construction de nouveaux échantillons.

Pour forcer cela, nous pouvons invoquer la divergence Kullback–Leibler (KL) dans la fonction de perte. La divergence $KL$ entre deux distributions de probabilité mesure simplement à quel point elles divergent l’une de l’autre. Minimiser la divergence $KL$ signifie ici optimiser les paramètres de distribution de probabilité ($\mu$ et $\sigma$) pour qu’ils ressemblent étroitement à ceux de la distribution cible.

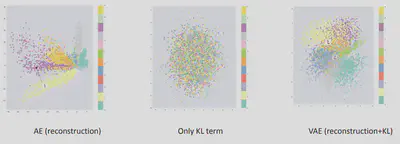
On remarque sur la figure précédente que, l’optimisation des deux ensemble, entraîne la génération d’un espace latent qui maintient la similitude des codages proches à l’ échelle locale via le regroupement, mais globalement il est très dense près de l’origine de l’espace latent.

Cela signifie que lors de la génération aléatoire, si nous échantillonnons un vecteur à partir de la même distribution antérieure des vecteurs codés, $Z_{0} \sim \mathcal{N}(0,1)$, le décodeur le décodera avec succès. Et si on interpole, il n’y a pas d’écarts soudains entre les clusters, mais un mélange homogène des caractéristiques qu’un décodeur peut comprendre.

En résumé, en plus de la modélisation du réseau du décodeur $p_{\theta}(x \mid z)$, on défini un réseau encodeur supplémentaire $q_{\theta}(x \mid z)$ qui se tente de se rapproche de la disitribution de $p_{\theta}(x \mid z)$.

Cela nous permet de dériver une limite inférieure sur la vraisemblance des données qui est traçable et que nous pouvons optimiser.

Maximiser la limite inférieure de la vraisemblance :

$$ \underbrace{\mathbf{E}_{z}\left[log p_{\theta}\left(x^{(i)} \mid z \right) \right]-D_{K L}\left(q_{\phi}\left(z \mid x^{(i)}\right) | p_{\theta}(z)\right)}_{\mathcal{L}\left(x^{(i)},\theta,\phi \right)} $$

6. Re-parametrization Trick

Pour entraîner le réseau VAE on utilise la descente de gradient. Pour cela, il faut que tous les calculs soient différentiables or l’échantillon $Z$ n’est pas différentiable. Ainsi, pour permettre la rétro-propagation, une solution consiste à utiliser un paramétrization trick pour que le gradient puisse se propager à travers le réseau.

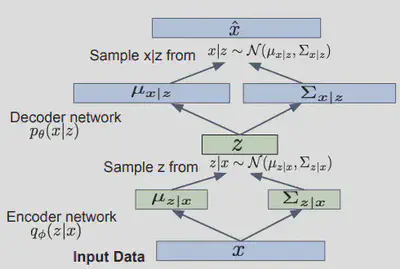
Re-parametrization trick:

$$ Si \quad Z_{0} \sim \mathcal{N}(0,1), alors \quad z=\mu_{x \mid z}+z_{0} \sqrt{\Sigma_{x \mid z}} \sim \mathcal{N}\left(\mu_{x \mid z}, \Sigma_{x \mid z}\right) $$

7. Conclusion: AE vs. VAE

Les auto-encodeurs standard apprennent à générer des représentations compactes et à bien reconstruire leurs entrées, mais à part quelques applications comme les auto-encodeurs de débruitage, ils sont assez limités.

Le problème fondamental avec les auto-encodeurs, pour la génération, est que l’espace latent dans lequel ils convertissent leurs entrées et où se trouvent leurs vecteurs codés, peut ne pas être continu ou permettre une interpolation facile.

Lorsqu’il s’agit de construire un modèle génératif, en fonction du cas d’usage on ne souhaite pas forcément apprendre à notre modèle à répliquer la même image qu’en entrée. En revanche on souhaite échantillonner de manière aléatoire à partir de l’espace latent ou générer des variations sur une image d’entrée à partir d’un espace latent continu.

Si l’espace présente des discontinuités (par exemple, des écarts entre les clusters) et que nous générons une variation, le décodeur générera simplement une sortie irréaliste, car le décodeur n’a aucune idée de la façon de traiter cette région de l’espace latent. Pendant l’entraînement, il n’a jamais vu de vecteurs codés provenant de cette région de l’espace latent.

Le VAE utilise un encodeur probabiliste pour modéliser la distribution des variables latentes plutôt que la variable latente elle-même. Avec un VAE la variance de l’espace latent peut être prise en compte dès la procédure d’échantillonnage. Cela élargit le pouvoir d’expression du VAE par rapport à l’AE simple dans la mesure où, même même si les données normales et les données “d’anomalie” peuvent partager une valeur moyenne identique, la variance peut différer. Les données “anormales” auront probablement une plus grande variance et présenteront une plus faible probabilité de reconstruction. Puisque les mappings déterministes des auto-encodeurs simples peuvent être considérés comme une mappage à la valeur moyenne, l’AE simple n’a pas la capacité de gérer la variance des données.